Digraph dengan Python

"Alhamdulillah luar biasa menyenangkan....". Itu ungkapan yang ada dalam diri saya ketika belajar pemrograman python. Kali ini penerapannya pada teori Digraph.

Anda yang pernah mengambil jurusan IPA ketika di SMA, saya rasa pernah mendapatkan teori Digraph (Directed Graph) pada mata pelajaran matematika. Berbeda dengan masa lalu yang mencoba teori digraph dari sudut pandang matematika. Kali ini saya sedang belajar digraph yang bersumber dari kuliah online MITx menggunakan pemrograman python, ternyata sangat asyik :).

Daripada bicara ngalor-ngidul, langsung saja deh. Digraph pada pembahasan ini diterapkan pada sebuah puzzle angka.


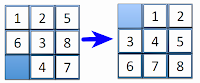
Diberikan sebuah puzzle sebagai berikut:

Tugas kita adalah menyusun puzzle yang ada di sebelah kiri sehingga sesuai dengan urutan seperti pada gambar di sebelah kanan.

Dengan menganggap ruang kosong sebagai angka '0' (Nol), maka kita dapat menyatakan bahwa puzzle yang tersedia adalah:

1  2  5
6  3  8
0  4  7

atau samadengan '125638047'

sedangkan target yang diinginkan adalah:

0  1  2
3  4  5
6  7  8

atau samadengan '012345678'

Selanjutnya eksekusi program di bawah ini. Masukkan kedua nilai di atas sebagai input:

======================================================================


class puzzle(object):
    def __init__(self, order):
        self.label = order
        for index in range(9):
            if order[index] == '0':
                self.spot = index
                return None
    def transition(self, to):
        label = self.label
        blankLocation = self.spot
        newBlankLabel = str(label[to])
        newLabel = ''
        for i in range(9):
            if i == to:
                newLabel += '0'
            elif i == blankLocation:
                newLabel += newBlankLabel
            else:
                newLabel += str(label[i])
        return puzzle(newLabel)
    def __str__(self):
        return self.label



def DFSWithGeneratorShortest(start, end, path = [], shortest = None):
    #assumes graph is a Digraph
    #assumes start and end are nodes in graph
    if start.label == end.label:
        return path
    for shift in shiftDict[start.spot]:
        new = start.transition(shift)
        if new.label not in path: #avoid cycles
            if shortest == None or len(path) < len(shortest):
                newPath = DFSWithGeneratorShortest(new,end,path,shortest)
                if newPath != None:
                    shortest = newPath
    return shortest


def BFSWithGenerator(start, end, q = []):
    initPath = [start]
    q.append(initPath)
    while len(q) != 0:
        tmpPath = q.pop(0)
        lastNode = tmpPath[len(tmpPath) - 1]
        if lastNode.label == end.label:
            return tmpPath
        for shift in shiftDict[lastNode.spot]:
            new = lastNode.transition(shift)
            if notInPath(new, tmpPath):
                newPath = tmpPath + [new]
                q.append(newPath)
    return None

def DFSWithGenerator(start, end, stack = []):
    #assumes graph is a Digraph
    #assumes start and end are nodes in graph
    initPath = [start]
    stack.insert(0, initPath)
    while len(stack)!= 0:
        tmpPath = stack.pop(0)
        lastNode = tmpPath[len(tmpPath) - 1]
        if lastNode.label == end.label:
            return tmpPath
        for shift in shiftDict[lastNode.spot]:
            new = lastNode.transition(shift)
            if notInPath(new, tmpPath): #avoid cycles
                newPath = tmpPath + [new]
                stack.insert(0, newPath)
    return None


def notInPath(node, path):
    for elt in path:
        if node.label == elt.label:
            return False
    return True


shiftDict = {}
shiftDict[0] = [1, 3]
shiftDict[1] = [0, 2, 4]
shiftDict[2] = [1, 5]
shiftDict[3] = [0, 4, 6]
shiftDict[4] = [1, 3, 5, 7]
shiftDict[5] = [2, 4, 8]
shiftDict[6] = [3, 7]
shiftDict[7] = [4, 6, 8]
shiftDict[8] = [5, 7]

ipuzzle = raw_input('Masukkan puzzle: ')
print ipuzzle[0],ipuzzle[1],ipuzzle[2]
print ipuzzle[3],ipuzzle[4],ipuzzle[5]
print ipuzzle[6],ipuzzle[7],ipuzzle[8]


igoal = raw_input('Masukkan target: ')
print igoal[0],igoal[1],igoal[2]
print igoal[3],igoal[4],igoal[5]
print igoal[6],igoal[7],igoal[8]

goal = puzzle(igoal)
test1 = puzzle(ipuzzle)

def printGrid(pzl):
    data = pzl.label
    print data[0], data[1], data[2]
    print data[3], data[4], data[5]
    print data[6], data[7], data[8]
    print ''

def printSolution(path):
    for elt in path:
        printGrid(elt)

path = BFSWithGenerator(test1, goal)
print '\nIterasi:\n\n',printSolution(path)


======================================================================
Program di atas akan secara otomatis menyusun puzzle sehingga sesuai dengan yang diinginkan. Anda dapat mengubah-ubah input puzzle dan target-nya. Namun apabila bilangan acak yang anda masukkan cukup kompleks, harap bersabar menunggu prosesnya :)

Selamat mencoba! :)